

Научно-технический интернет-журнал Свидетельство о регистрации Эл № ФС 77-31314
 |
 |
Главная | E-mail | 27.07.2024 |
|
|
||
| Главная страница | О журнале | Авторам | Редколлегия | Контакты | ||
|
|
||
|
Научно-технический интернет-журнал Свидетельство о регистрации Эл № ФС 77-31314 |
||
|
Обработка видеосигнала
Дата публикации : 06.02.2009 | Просмотров : 1808 |
Использование WAVELET-преобразования в алгоритме сжатия изображения JPEG. УДК 621.391.019
Санкт-Петербургский Государственный политехнический университет
Проводится оценка возможности применения wavelet-преобразования в алгоритме JPEG вместо дискретного косинусного преобразования. Предложен модифицированный алгоритм JPEG с использованием wavelet - преобразования, позволяющий обеспечить предварительный просмотр копии всего изображения путем обработки лишь части данных. Приводится пример реализации модифицированного алгоритма JPEG на базе цифрового сигнального процессора TMS320VC5510 применительно к беспроводной системе видеонаблюдения.
Введение
При построении беспроводных систем видеонаблюдения, использующих низкоскоростные каналы связи, возникает необходимость передачи больших объемов данных (изображений) за ограниченное время. Для этого обычно используется алгоритм сжатия изображений JPEG [1], обеспечивающий степень сжатия от 2 до 200 раз. Однако, в ряде случаев, например, в беспроводных охранных системах видеонаблюдения нет необходимости передавать по каналу связи данные о каждом полном изображении. Можно использовать режим предварительного просмотра изображений. При реализации такого режима объем передаваемых данных существенно уменьшается.
Базовый алгоритм сжатия изображений.
В качестве базового алгоритма рассмотрим применение алгоритма JPEG [1]. Характеристики алгоритма: степень сжатия варьируется от 2 до 200, алгоритм ориентирован на сжатие полноцветных (с глубиной цвета 24 бита, по 8 бит на каждую из 3-х компонент) изображений или изображений в градациях серого без резких переходов цветов. Алгоритм оперирует областями 8x8 точек, на которых яркость и цвет меняются сравнительно плавно. Вследствие этого при применении к матрице такой области дискретного косинусного преобразования (ДКП) значимыми оказываются только первые коэффициенты. Таким образом, сжатие в JPEG осуществляется за счет плавности изменения цветов в изображении. Структурная схема алгоритма JPEG представлена на рис.1.
В блоке "RGB в YCbCr" происходит преобразование цветовых пространств. YCbCr представляет собой аппаратно-ориентированную модель, используемую в телевидении и служащую для сокращения передаваемой полосы частот за счет использования психофизиологических особенностей зрения. В этой модели Y - интенсивность цвета, а Cb и Сr - синяя и красная цветоразностные компоненты. Кодирование изображений в этой палитре существенно уменьшает количество информации, требуемой для воспроизведения изображения без существенной потери его качества. Для преобразования палитры RGB в YCbCr пользуются следующими соотношениями:
Блок "ДКП" является ключевым компонентом работы алгоритма. ДКП представляет собой разновидность преобразования Фурье и также имеет обратное преобразование. Графическое изображение можно рассматривать как совокупность пространственных волн, причем оси X и Y совпадают с шириной и высотой картинки, а по оси Z откладывается значение цвета соответствующего пикселя изображения. ДКП позволяет переходить от пространственного представления картинки к ее спектральному представлению и обратно. Воздействуя на спектральное представление картинки, состоящее из "гармоник", то есть, отбрасывая наименее значимые из них, можно балансировать между качеством воспроизведения и степенью сжатия. Формула дискретного косинусного преобразования представлена ниже:
Время, необходимое для вычисления каждого элемента матрицы дискретного косинусного преобразования, зависит от ее размера. Одной из особенностей является то, что практически невозможно выполнить дискретное косинусное преобразование для всего изображения сразу. В качестве решения этой задачи необходимо разбивать изображение на блоки размером 8x8 точек. В блоке "Квантование" происходит деление рабочей матрицы на матрицу квантования поэлементно с округлением элементов до целого значения. Для каждой компоненты (Y, Cr и Cb) в общем случае задается своя матрица квантования q[x,y]:
В блоке "Зигзаг" - сканирование" происходит перевод матрицы размером 8x8 точек в 64-элементный вектор при помощи "зигзаг"-сканирования. Таким образом, начальными элементами вектора являются коэффициенты матрицы, соответствующие низким частотам, а конечными - высоким частотам. В блоке "RLE" происходит операция свертывания полученного вектора с помощью алгоритма группового кодирования RLE. В результате получаются пары типа <пропустить, число>, где "пропустить" является количеством пропускаемых нулей, а "число" - значение, которое необходимо поставить в следующую ячейку. В блоке "сжатие по Хаффману" происходит свертывание получившихся пар кодированием по Хаффману с фиксированной таблицей. Процесс восстановления изображения в этом алгоритме полностью симметричен.
Вейвлет-преобразование
Вейвлеты представляют собой математические функции, позволяющие анализировать различные частотные компоненты данных. Вейвлеты обладают существенными преимуществами по сравнению с преобразованием Фурье, потому что вейвлет-перобразование позволяет судить не только о частотном спектре сигнала, но также о том, в какой момент времени появилась та или иная гармоника. С их помощью можно легко анализировать прерывистые сигналы, либо сигналы с острыми всплесками. Кроме того, вейвлеты позволяют анализировать данные согласно масштабу, на одном из заданных уровней. Уникальные свойства вейвлетов позволяют сконструировать базис, в котором представление данных будет выражаться всего несколькими ненулевыми коэффициентами. Это свойство делает вейвлеты очень привлекательными для упаковки данных, в том числе видео- и аудио-информации. Вейвлеты нашли широкое применение в цифровой обработке изображения, обработке сигналов и анализе данных. Существует два класса вейвлет-преобразований: непрерывные и дискретные. Непрерывное вейвлет-преобразование (CTWT) есть скалярное произведение f(x) и базисных функций
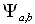 являются вещественными и колеблются вокруг оси абсцисс. Они определены на некотором интервале. Данные функции называются вейвлетами и могут рассматриваться как масштабированные и сдвинутые версии функции-прототипа являются вещественными и колеблются вокруг оси абсцисс. Они определены на некотором интервале. Данные функции называются вейвлетами и могут рассматриваться как масштабированные и сдвинутые версии функции-прототипа 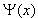 . Параметр b показывает расположение во времени, а а - параметр масштаба. Большие значения а соответствуют низким частотам, малые - высоким. . Параметр b показывает расположение во времени, а а - параметр масштаба. Большие значения а соответствуют низким частотам, малые - высоким.
Алгоритм вейвлет-преобразования может быть представлен, как передача сигнала через пару фильтров: низкочастотный и высокочастотный. Низкочастотный фильтр выдает грубую форму исходного сигнала. Высокочастотный фильтр выдает сигнал разности или дополнительной детализации. На практике вейвлет-преобразование должно применяться к сигналам конечной длины. Таким образом, его необходимо модифицировать, чтобы из сигнала конечной длины получать последовательность коэффициентов той же длины. Алгоритм дискретного вейвлет-преобразования можно представить как субполосное преобразование с фильтрацией и последующим прореживанием в два раза. Так как в данном случае имеется два фильтра H и G, то банк фильтров - двухполосный и может быть изображен, как показано на рис. 2.
В обработке изображений используется двумерное дискретное вейвлет-преобразование, которое представляет собой одномерное вейвлет-преобразование по очереди применяемое к столбцам, а затем к строкам. Можно представить вейвлет-преобразование изображения следующей структурой на основе банков фильтров представленной на рис. 3.
Сравнение с другими алгоритмами сжатия изображений
Преимущество применения вейвлет-преобразования вместо ДКП (шаг 3 в алгоритме JPEG) состоит в том, что вейвлет-преобразованию подвергается изображение целиком, а не его отдельные фрагменты. Также применение вейвлет-преобразования позволяет реализовать функции предварительного просмотра и масштабирования изображения. В левом верхнем углу преобразованного изображения хранится уменьшенная копия исходного изображения (см. рис. 4). Для реализации режима предварительного просмотра изображения достаточно передать лишь эти данные.
Модифицированный алгоритм сжатия изображений JPEG с использованием вейвлет-преобразования
В модифицированном алгоритме JPEG вместо ДКП использовано дискретное вейвлет-преобразование. В качестве элементной базы рассматривался цифровой сигнальный процессор TMS320VC5510 компании Texas Instruments [5]. Данный микропроцессор обладает высокой производительностью при низком энергопотреблении. Библиотека обработки изображений состоит из более чем 20 подпрограмм, оптимизированных для ядра C55x [6]. Библиотека включает в себя стандартные функции обработки изображений, такие, как сжатие, обработка видеосигнала, машинное зрение и медицинские задачи обработки изображений. В частности, библиотека включает в себя функции, реализующие вейвлет-преобразование, квантование и процедуру сжатия по Хаффману, которые используются в разработанной модификации алгоритма.
С помощью разработанной программы были сжаты тестовые изображения. Степень сжатия составила 5-10 раз, т.е. меньше, чем при использовании дискретного косинусного преобразования. При замене дискретного косинусного преобразования на вейвлет-преобразование применение группового кодирования перед сжатием по Хаффману не обеспечивает должного сжатия. Это объясняется тем, что при разложении дискретным косинусным преобразованием большинство высокочастотных коэффициентов в матрице 8х8 после квантования равны нулю, что при групповом кодировании дает большой коэффициент сжатия. При использовании вейвлет-преобразования такого эффекта не наблюдается. Матрицы коэффициентов после квантования имеют примерно одинаковые значения, что при групповом кодировании не даёт уменьшения в размере. Степень сжатия можно увеличить путем замены группового кодирования на иной алгоритм сжатия. В процессе работы алгоритма необходимо хранить в памяти матрицу исходного изображения и матрицу цветовой компоненты, которая обрабатывается в данный момент. Также необходимо зарезервировать область памяти для хранения сжатого изображения. Таким образом, для работы алгоритма необходимо около 800 Кбайт памяти. В микропроцессоре TMS320VC5510 доступно около 300 Кбайт внутренней памяти, поэтому была использована внешняя память SDRAM. Производительность алгоритма составляет 2 кадра в секунду.
Заключение
Литература
|
| ||||||||