Россия, Санкт-Петербург http://www.telephototech.ru
| Дата публикации : 14.04.2008 |
Автор(ы) : Ярышев С.Н., Горбачев А.А., Краснящих А.В., Тимофеев А.Н.
Рассматриваются варианты реализации алгоритма определения координат на матрице приборов с зарядовой связью. Предлагается методика пересчета координат, полученных в измерительном приборе, в систему, связанную с контролируемым объектом, для распределенной оптико-электронной системы, основанной на контрольном элементе с парой полупроводниковых излучающих диодов.
Все более широкое применение при бесконтактном измерении смещений контролируемых объектов находят распределенные оптико-электронные системы, состоящие из нескольких измерительных каналов. Каждый из таких каналов включает в себя базовый блок с матричным приемником излучения и контрольный элемент (КЭ), выполненный в виде излучателя или отражателя [1,2]. Высокая точность линейных измерений в таких системах обеспечивается геометрическими характеристиками растра приемников с зарядовой связью (ПЗС). Эта особенность позволяет, несмотря на дискретный характер ПЗС-структуры в плоскости анализа изображения, регистрировать линейные смещения изображения с погрешностью до десятых и сотых долей пространственного периода элементов [3,4].
Целью статьи является показать особенности пересчета приборных координат в систему, связанную с объектом контроля в измерительном канале распределенной оптико-электронной системы контроля смещений, основанной на использовании контрольного элемента с парой полупроводниковых излучающих диодов (ПИД).
Задачу определения смещения КЭ, жестко закрепленного на контролируемом объекте, с помощью матрицы ПЗС в общем случае можно разбить на несколько независимых этапов:
- предварительная фильтрация полученного изображения;
- выделение изображения КЭ;
- определение координат изображения на матрице ПЗС;
- пересчет полученных координат из системы координат связанной с плоскостью изображений в систему координат, связанную с пространством предметов.
В рассматриваемом канале на этапе предварительной фильтрации решается обычная задача подавления шумов и повышения отношения сигнал/шум, в то время как на этапе выделения изображения КЭ производится обнаружение объекта и грубая оценка его параметров. После нахождения изображения КЭ вокруг него выделяется область, которая позволяет уменьшить количество обрабатываемых данных. Далее производится определение координат КЭ на ПЗС приемнике, а затем процедура их восстановления.
Одним из первых этапов обработки изображений в цифровых оптико-электронных системах является дискретизация исходных изображений по пространственным координатам, а так же квантование по уровню отсчетных значений яркости или освещенности его отдельных элементов [5].
Обычно, в качестве модели распределения освещенности по изображению точечного излучателя рассматриваются некоторые функциональные зависимости типа косинусной или функции Гаусса. Зависимость в виде гауссоиды вращения, при моделировании используется наиболее широко, так как ближе других к действительности и позволяет аналитически оценить погрешность определения координат изображения.
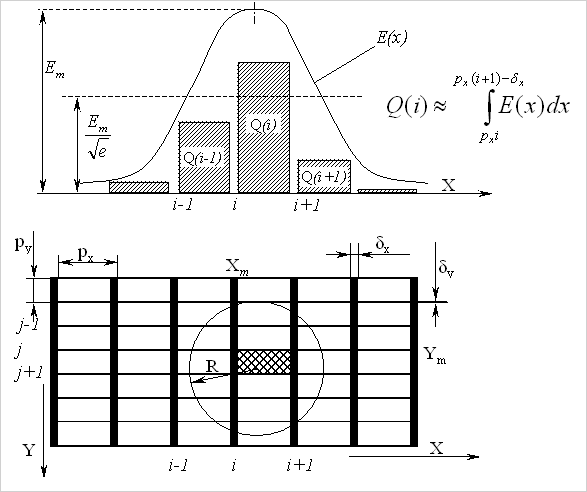
Рис. 1. Распределение освещенности на фоточувствительной площадке ПЗС и формирование зарядового рельефа
На рис. 1 представлено распределение двумерной непрерывной функции освещенности в плоскости анализа E(x,y) вдоль оси X. Эта функция преобразуется фотоприемником на ПЗС в дискретную функцию U(i,j), которая после процесса квантования по уровню преобразуется в матрицу [Eij].
Позиционную чувствительность ПЗС матрицы можно повысить за счет интерполяции сигналов, снимаемых со смежных элементов.
Одним из наиболее простых интерполяционных алгоритмов определения координат точечного объекта является алгоритм энергетического центра ("центра тяжести") [3].
При малых отношениях сигнал/шум наиболее предпочтительными являются другие алгоритмы. Сущность таких алгоритмов после определения координат элемента с максимальным уровнем сигнала сводиться к следующему:
- осуществляется восстановление путем интерполяции непрерывной функции U(x,y), адекватной распределению освещенности в плоскости анализа E(x,y);
- производится вычисление частных производных ∂U(x,y)/∂x и ∂U(x,y)/∂y с последующим вычислением оценок в результате решения уравнений (1):
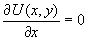 ,
, 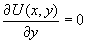 . (1)
. (1)
Восстановление двумерной функции U(x,y) требует выполнения большого числа вычислительных операций, поэтому для уменьшения количества вычислений, возможно, производить интерполирование таблично заданных функций UYm(x) и UXm(y), то есть значения выбираются из столбца и строки содержащей элемент с максимальной освещенностью. Поиск экстремума в таком случае можно производить, например, методами дихотомии, золотого сечения, по знаку первой производной и т.д.
Для создания измерительной системы, адаптивной к изменению дистанции необходимо иметь априорную информацию о расстоянии между измерительным блоком и КЭ, либо иметь некоторый эталон смещения КЭ [6].
В качестве базового варианта рассмотрим коллимационный вариант реализации оптической части измерительного канала и метод определения координат КЭ 2 (рис. 2), т.к. полученные выкладки будут иметь место и в других случаях реализации оптической части измерительного канала. В таком варианте в качестве контрольного элемента используется пара ПИД 1, а в качестве приемника оптического излучения используется матричный ФПЗС 4 с объективом 3. Следует помнить, что фотоприемник имеет матричную структуру с конечными размерами фоточувствительных элементов и промежутками нечувствительности между ними. В момент измерения программа включает поочередно только один из пары излучающих диодов 1 (рис. 2).
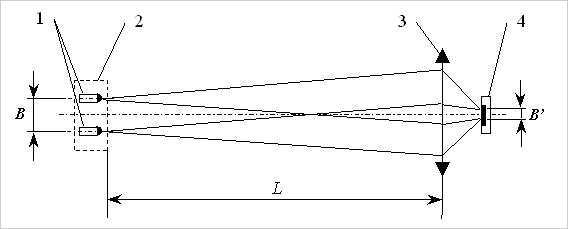
Рис. 2. Общая схема оптической части измерительного канала оптико-электронной системы
Координаты середины отрезка между ПИД 1, принимаемые как координаты КЭ 2 (x,y), установленного на объекте контроля, связаны с координатами изображения КЭ 2 (x’ ,y’ ) следующими выражениями:
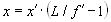 и
и  , (2)
, (2)
где L - расстояние от контрольного элемента до объектива, f’ - заднее фокусное расстояние объектива системы.
В рассматриваемом случае в формуле (2) присутствует выражение (L/f ’ -1), которое не позволяет реализовать автоматически калибрующуюся измерительную систему, без введения в нее дополнительных устройств изменения дистанций до КЭ и фокусного расстояния. Фокусное расстояние в конкретной системе изменяется мало, однако дистанция от КЭ до измерительного блока может изменяться в широких пределах, и это необходимо учитывать в процессе измерения смещений. Для устранения этого предлагается использовать схему, в которой КЭ представлен в виде пары точечных источников, расположенных в одной плоскости, расстояние между которыми известно с большой точностью (или может быть выяснено в процессе юстировки системы).
В распределенной оптико-электронной системе используется КЭ с парой точечных источников, расстояние между которыми известно [7]. По величине этого расстояния осуществляется автокалибровка смещения КЭ измерительной системы.
Расстояние между ПИД 1 B известно с определенной точностью. База B и её изображение B’ связаны соотношением:
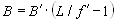 . (3)
. (3)
Из рис. 3 по теореме Пифагора получим для B′ выражение:
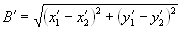 , (4)
, (4)
где (x′1,y′1) и (x′2,y′2) - координаты центров изображения точечных объектов, входящих в состав КЭ 2, B′ - сформированная измерительная база, B′х и B′у - проекции измерительной базы на координатные оси X и Y соответственно, a ′ - угол между измерительной базой и координатной осью Х, а рх - горизонтальный размер фоточувствительной площадки одного элемента матричного приемника с включенной зоной нечувствительности, расположенной слева (либо справа) от элемента, ру - вертикальный размер фоточувствительной площадки одного элемента матричного приемника с включенной зоной нечувствительности, расположенной снизу (либо сверху) от элемента.
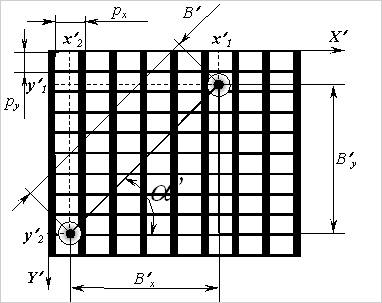
Рис. 3. Схема наложения системы координат плоскости анализа на матричную структуру
Таким образом, из (3) и (4) получим:
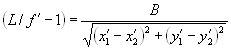 . (5)
. (5)
Из выражения (5) видно, что значение величины (L/f ’ -1) можно получить в процессе измерений без введения дополнительного канала измерения дистанций, если величина B известна до начала измерений. В этом случае B′ вычисляется из соотношения (4) в процессе измерений координат ПИД 1 (рис. 2), входящих в состав КЭ 2.
При проведении измерений в оптико-электронной системе достаточно важен процесс восстановления координат изображения, сформированного приемником оптического излучения, поэтому в качестве приемника используется матричный фотоприемник на основе ПЗС.
После процедуры оцифровки видеосигнал, снимаемый с матричного ПЗС, записывается в оперативное запоминающее устройство (ОЗУ) блока, выполняющего обработку оцифрованного изображения с целью получения координат центров изображений ПИД. На рис. 4 изображен вид условной системы координат, связанной с изображением излучающих диодов 1 (рис. 2), находящейся в ОЗУ.
Координаты (x1 ПЗС, y1 ПЗС) и (x2 ПЗС, y2 ПЗС) на рис. 4 вычислены по некоторому алгоритму, например, методом определения энергетического центра тяжести, первого и второго ПИД. BПЗС - сформированная измерительная база, Bх ПЗС и Bу ПЗС - проекции измерительной базы на координатные оси XПЗС и YПЗС соответственно, a ПЗС - угол между измерительной базой и координатной осью ХПЗС.
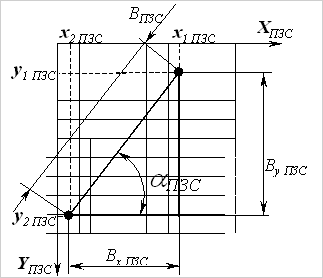
Рис. 4. Условная система координат, связанная с изображениями ПИД, которые находятся в ОЗУ
После выполнения оцифровки видеокадра, сформированного фотоприемником на ПЗС, и записи его в ОЗУ, теряется информация о величине шага элементов ПЗС рх и ру, что приводит к линейным искажениям, поэтому необходимо проводить процедуру восстановления координат. Координаты в плоскости анализа связаны с условными координатами (координатами, находящимися в ОЗУ) соотношениями [1]:
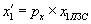 и
и 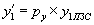 , (6)
, (6)
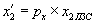 и
и 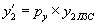 . (7)
. (7)
В результате, из сказанного выше соотношение (5) принимает вид:
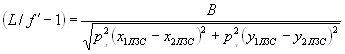 , (8)
, (8)
при этом стоит отметить, что B - известный параметр, значения x1 ПЗС, y1 ПЗС, x2 ПЗС, y2 ПЗС определяются в результате измерения, а коэффициенты рх и ру определяются из параметров фотоприемника на ПЗС или уточняются в процессе юстировки системы. Таким образом, осуществляется автокалибровка измерительной системы.
Подставляя значение для (L/f ’ -1) из (8) в соотношения (2) и учитывая (6) и (7), получаем зависимости, связывающие координаты КЭ в пространстве изображений, с координатами изображений, сформированными матричным приемником:
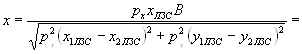
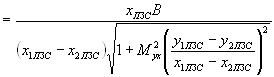 , (9)
, (9)
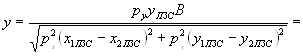
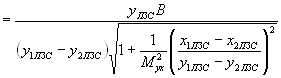 . (10)
. (10)
где Myx = py /px - коэффициент линейного искажения.
Таким образом, если при измерениях не будет происходить скручивания, при которых изображения ПИД будут находиться на одной вертикальной или горизонтальной прямых, то в расчетах удобнее использовать вариант с параметром Myx. Этот параметр определяется из характеристик матрицы и может уточняться в процессе калибровки системы.
Приведенная методика определения соответствия между линейными смещениями КЭ, а, следовательно, и самого объекта (КЭ жестко закреплен на контролируемом объекте), и регистрируемыми информативными величинами, позволяет отказаться от измерения дистанции при регистрации смещений КЭ, что позволит уменьшить погрешность и автоматизировать процесс измерений.
СПИСОК ЛИТЕРАТУРЫ
- Коротаев В.В, Краснящих А.В. Исследование макета оптико-электронной системы контроля деформации крупногабаритных инженерных сооружений // V Международная конференция Прикладная оптика 15-17 октября 2002 г. Санкт-Петербург. Россия. Сборник трудов. Т.1. Оптическое приборостроение. СПб: Труды оптического общества им. Д.С. Рождественского, 2002. - c.70-74.
- Иванов А.Г., Коротаев В.В., Краснящих А.В. О построении оптико-электронных систем контроля прогиба. // Научно-технический вестник СПб ГИТМО (ТУ). Выпуск 5. Оптические приборы, системы и технологии / Главный редактор В. Н. Васильев. СПб: СПб ГИТМО (ТУ), 2002. с. 100-104.
- Андреев А.Л., Ярышев С.Н., Стрелков А.Р. Аппаратные и программные средства оптико-электронных приборов с телевизионными датчиками на ФПЗС: Методическое указание. - СПб: ИТМО, 1995, с. 49.
- Твердотельное телевидение: Телевизионные системы с переменными параметрами на ПЗС и микропроцессорах /Хромов Л.И., Лебедев Н.В., Цыцулин А.К., Куликов А.Н. /Под ред. И.А. Росселевича. - М.: Радио и связь, 1986, c.184.
- Дегтярев С.В., Садыков С.С., Тевс С.С., Ширабакина Т.А. Методы цифровой обработки изображения: Учебное пособие. Ч.1 /Курск, Гос. техн. ун-т. Курск, 2001, c.167.
- Горбачев А.А., Коняхин И.А., Тимофеев А.Н. Исследование погрешности измерения поперечных смещений распределенной автоколлимационной системой контроля деформаций при изменениях яркости источников. //Научно-технический вестник СПб ГИТМО (ТУ), Вып. 9. /Под ред. Ю.А. Гатчина, СПб: СПб ГИТМО (ТУ), 2003, с. 73-78.
- Горбачев А.А., Прокофьев А.В., Тимофеев А.Н. Особенности выбора параметров оптической схемы распределенной оптико-электронной системы контроля смещений //Сборник трудов пятой международной конференции Прикладная оптика 15-17 октября 2002 г. СПб. ГОИ Т.1, c. 84-87.
|
Внимание !
Использование любых текстовых или графических материалов(а так-же их фрагментов) с сайта http://www.telephototech.ru возможно с разрешения администрации сайта с обязательным указанием ссылок на первоисточник и авторов статей и публикаций ! |
|
ТелеФото Техника Copyright © 2024 |
ТелеФото Техника Россия, Санкт-Петербург, 195253 Салтыковская дорога д.18 |
http://www.telephototech.ru E-mail: infos@evs.ru |
